Updated on 2017-04-12
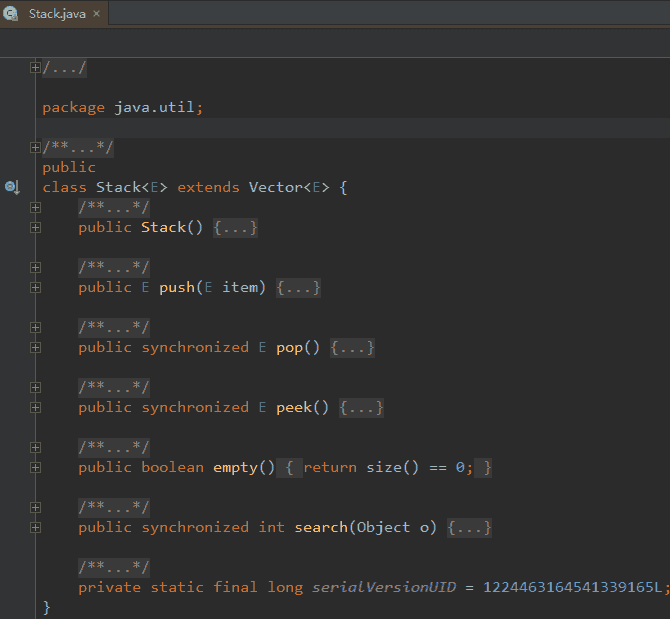
- 数据结构:相互之间存在一种或多种特定 关系 的数据元素的 集合。
- 队列(两个口)(Queue):先进先出(FIFO, First In First Out),队头 ⟺ 队尾。
- 普通队列(劣),环形队列(优)。
- 堆栈(一个口)(Stack):先进后出(LIFO, Last In First Out),栈顶 ⟺ 栈底。
- push:数据入栈。
- pop:数据出栈,并作为此函数的值返回该对象。
- peek:查看栈顶部的对象,但不从栈中移除它。
- empty:测试栈是否为空。
- search:返回对象在栈中的位置。
- 队列(两个口)(Queue):先进先出(FIFO, First In First Out),队头 ⟺ 队尾。
双端队列
import java.util.ArrayDeque;
public class A {
private static ArrayDeque<Integer> deque = new ArrayDeque<>(); 双端队列(ArrayDeque 非线程安全,LinkedBlockingDeque 线程安全)
public static void main(String[] args) {
System.out.println("队列");
deque.offerLast(1);
deque.offerLast(2);
deque.offerLast(3);
deque.offerLast(4);
show();
deque.offerLast(deque.pollFirst());
show();
deque.offerLast(deque.pollFirst());
show();
deque.offerLast(deque.pollFirst());
show();
deque.offerLast(deque.pollFirst());
show();
System.out.println("————————");
deque.clear(); 清空双端队列
System.out.println("堆栈");
deque.offerFirst(1);
deque.offerFirst(2);
deque.offerFirst(3);
deque.offerFirst(4);
show();
deque.offerFirst(deque.pollFirst());
show();
deque.offerFirst(deque.pollFirst());
show();
deque.offerFirst(deque.pollFirst());
show();
deque.offerFirst(deque.pollFirst());
show();
}
private static void show() {
deque.forEach(i -> System.out.print(i + " "));
System.out.println();
}
}
----
输出:
队列
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
1 2 3 4
————————
堆栈
4 3 2 1
4 3 2 1
4 3 2 1
4 3 2 1
4 3 2 1
import java.util.ArrayDeque;
public class A {
public static void main(String[] args) {
String[] strs = new String[]{"A", "B", "C"};
ArrayDeque<String> deque = new ArrayDeque<>();
final int k = 2;
for (String s : strs) {
deque.addFirst(s);
System.out.printf(space(k * deque.size()) + "<%s>\n", s);
}
for (int j = 0, n = deque.size(); j < n; j++) {
System.out.printf(space(k * deque.size()) + "</%s>\n", deque.removeFirst());
}
}
private static String space(int i) {
StringBuilder sb = new StringBuilder();
for (int j = 0; j < i; j++) {
sb.append(" ");
}
return sb.toString();
}
}
----
输出:
<A>
<B>
<C>
</C>
</B>
</A>
固定顺序进栈,求出栈顺序总数
1 个元素进栈有 1 种出栈顺序,2 个元素进栈有 2 种出栈顺序,3 个元素进栈有 5 种出栈顺序
把 n 个元素的出栈顺序数记为 f(n),则对于 1、 2、 3 元素可得出:
- f(1) = 1 // 1
- f(2) = 2 // 12、21
- f(3) = 5 // 123、213、231、312、321
那么对于 f(4),给其 4 个元素编号为 a,b,c,d;假设进栈顺序为 abcd,考虑出栈顺序元素 a 出现在1号位置、2号位置、3号位置、4号位置的情况:
- a 在1号位置:只可能 a 进栈,再马上出栈;还剩 b,c,d,即子问题
f(3)。 - a 在2号位置:有1个元素比 a 先出栈,即子问题
f(1)(只能是 b);还剩 c,d,即子问题f(2);那么一共的顺序个数为f(1)*f(2)。 - a 在3号位置:有2个元素比 a 先出栈,即子问题
f(2)(只能是 b,c);还剩 d,即子问题f(1);那么一共的顺序个数为f(2)*f(1)。 - a 在4号位置:a 最后出栈,即求前面 b,c,d 的出栈顺序,即子问题
f(3)。
结合所有情况,即:f(4) = f(3) + f(1)*f(2) + f(2)*f(1) + f(3)
再规整化,定义 f(0) = 1,即:f(4) = f(0)*f(3) + f(1)*f(2) + f(2)*f(1) + f(3)*f(0)
再推广至 n,即:f(n) = f(0)*f(n-1) + f(1)*f(n-2) + … + f(n-2)*f(1) + f(n-1)*f(0)
化简为递推公式:
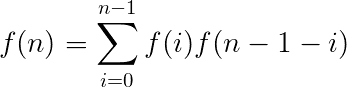
推出通项公式:
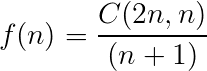
中缀表达式转后缀表达式的思路
- stack1 ⟺ 操作符;stack2 ⟺ 操作数
- 操作符:若 stack1 为空栈,则直接进栈 stack1。
- 若优先级比 stack1 栈顶元素高,则进栈 stack1。
- 若优先级比 stack1 栈顶元素低或相同,则弹出 stack1 栈顶元素至 stack2,再与 stack1 栈顶元素比较。
- 操作数:直接进栈 stack2。
- 最后清空 stack1 元素至 stack2,done。
Reference
Catalan number:https://en.wikipedia.org/wiki/Catalan_number
Regex:http://help.mythicsoft.com/filelocatorpro/cn/quickstart.htm , Java
LaTeX:https://latex.codecogs.com/eqneditor/editor.php
10进制 转 2进制
----
public class A {
public static void main(String[] args) {
System.out.println(conversion(6, 2)); 6 转为 2进制
}
private static StringBuilder conversion(int num, int n) {
Stack<Integer> stack = new Stack<Integer>(); 新建一个栈
for (; ; ) {
stack.push(num % n); 余数入栈
num /= n;
if (num == 0) {
break;
}
}
return new StringBuilder(stack.toString()).reverse(); ①
}
}
注 ①:
1
1
0 ➜ [0, 1, 1] ➜ ]1 ,1 ,0[
----
输出:
]1 ,1 ,0[
-------------------------------------------------------
括号配对问题(消消乐)
----
public class A {
public static void main(String[] args) {
System.out.println(isMatch("(])"));
System.out.println(isMatch("([[]()])"));
}
private static boolean isMatch(String str) {
Stack<Character> stack = new Stack<Character>(); 新建一个栈
for (int i = 0; i < str.length(); i++) { 扫描字符串
switch (str.charAt(i)) {
case '(':
stack.push('('); 数据入栈
break;
case '[':
stack.push('['); 数据入栈
break;
case ')':
if (!stack.empty() && stack.pop() == '(') { 匹配成功,数据出栈
continue;
} else {
return false;
}
case ']':
if (!stack.empty() && stack.pop() == '[') { 匹配成功,数据出栈
continue;
} else {
return false;
}
}
}
return stack.empty(); 判断栈是否为空(其实到这步可以直接返回 true)
}
}
----
输出:
false
true
-------------------------------------------------------
中缀表达式转为后缀表达式
----
public class A {
public static void main(String[] args) {
String a = "1.8 + 5 / 8 * 1.6";
System.out.println(a + "\n" + reverse(a));
}
private static String reverse(String str) {
Stack<String> stack = new Stack<>(); stack 原表达式
Stack<String> stack1 = new Stack<>(); stack1 操作符
Stack<String> stack2 = new Stack<>(); stack2 操作数
for (String i : reverseString(str.split(" "))) { 字符串 ➜ String 数组 ➜ 反转 ➜ 压入 stack
stack.push(i);
}
for (; !stack.empty(); ) { stack(空) ➜ stack1 和 stack2
String i = stack.peek(); 预览栈顶元素
switch (i) {
case "+": 同一优先级操作符(低)
case "-":
if (stack1.empty()) { 空栈直接进栈
stack1.push(stack.pop());
} else { 否则清空 stack1 至 stack2,再进栈
for (; !stack1.empty(); ) {
stack2.push(stack1.pop());
}
stack1.push(stack.pop());
}
break;
case "*": 同一优先级操作符(高)
case "/":
if (stack1.empty() || stack1.peek().equals("+") || stack1.peek().equals("-")) {
stack1.push(stack.pop());
} else { 空栈直接进栈或者优先级比 stack1 栈顶元素高,否则弹出 stack1 栈顶元素至 stack2,再与 stack1 栈顶元素比较
stack2.push(stack1.pop());
}
break;
default: 操作数直接进栈 stack2
stack2.push(stack.pop());
break;
}
}
for (; !stack1.empty(); ) { stack1(空) ➜ stack2
stack2.push(stack1.pop());
}
String[] strings = new String[stack2.size()];
for (int i = 0, j = stack2.size(); i < j; i++) { stack2(空) ➜ String 数组
strings[i] = stack2.pop();
}
String string = "";
for (String i : reverseString(strings)) { String 数组 ➜ 反转 ➜ 字符串
string += i + " ";
}
return string;
}
private static String[] reverseString(String[] str) { 反转数组
String[] strings = new String[str.length];
for (int i = 0, j = str.length; i < j; i++) {
strings[i] = str[str.length - i - 1];
}
return strings;
}
}
----
输出:
1.8 + 5 / 8 * 1.6
1.8 5 8 / 1.6 * +
-------------------------------------------------------
后缀表达式求值
----
public class A {
public static void main(String[] args) {
String a = "1.8 5 8 / 1.6 * +";
System.out.println(calculate(a));
}
private static String calculate(String str) {
if (str.matches(".*0 /.*-.*")) { 使用正则表达式匹配除以0,分别返回 "-∞" 或 "∞"
return "-∞";
} else if (str.matches(".*0 /.*+.*")) {
return "∞";
}
Stack<String> stack = new Stack<>();
double a, b;
for (String i : str.split(" ")) { 字符串 ➜ String 数组 ➜ 扫描
switch (i) {
case "+": 操作符则弹出栈顶2个元素进行运算,再将结果进栈
a = Double.parseDouble(stack.pop()); String ➜ double
b = Double.parseDouble(stack.pop());
stack.push(String.valueOf(b + a)); double ➜ String
break;
case "-":
a = Double.parseDouble(stack.pop());
b = Double.parseDouble(stack.pop());
stack.push(String.valueOf(b - a));
break;
case "*":
a = Double.parseDouble(stack.pop());
b = Double.parseDouble(stack.pop());
stack.push(String.valueOf(b * a));
break;
case "/":
a = Double.parseDouble(stack.pop());
b = Double.parseDouble(stack.pop());
stack.push(String.valueOf(b / a));
break;
default: 操作数直接进栈
stack.push(i);
break;
}
}
return stack.pop();
}
}
----
输出:
2.8